|
|
|
|
|
|
|
Tous les chiffres sont égaux ?
Pacôme rencontre Aristide, et lui propose un pari.
"Ce livre contient la liste de toutes les communes de France, avec leur surface, en mètres carrés."
"Je te propose le jeu suivant. On ouvre le livre au hasard, et on pointe au hasard sur une commune. On regarde le nombre de ses habitants, et plus précisément, le premier des chiffres composant ce nombre. Si ce chiffre est supérieur ou égal à 5, je t'offre à boire. Sinon, c'est toi qui régales.
Es-tu d'accord ?"
Aristide fait mentalement le raisonnement suivant: il y a neuf chiffres possibles pour débuter un nombre. Cinq d'entre eux me font gagner, les quatre autres font gagner Aristide. J'ai donc un peu plus de chances de gagner qu'Aristide:
"je vais accepter le pari".
Que pensez-vous du raisonnement d'Aristide ?
Montrer/cacher la solution de cette énigme
La solution de l'énigme Tous les chiffres sont égaux ? :
Le raisonnement d'Aristide est faux, car il est basé sur le fait que le premier chiffre du nombre d'habitants d'une commune française a autant de chances d'être un "1" plutôt qu'un "2", ou un "3", etc.. En fait, plus le chiffre est petit, plus il a de chances de figurer en tête du nombre. Ce n'est pas une particularité des communes françaises: la même propriété se retrouverait avec n'importe quelle autre liste de valeurs, par exemple, la surface des îles du Pacifique, ou la hauteur des montagnes d'Asie. Ce phénomène est connu sous le nom de "loi de Benford": la probabilité qu'un nombre commence par n est égale à Log(n+1)-Log(n), Log étant le logarithme décimal. On en conclut qu'Aristide a moins de 40% de chances de gagner, alors qu'il croyait en avoir plus de 55% ! A défaut d'une explication mathématique rigoureuse, on se contentera d'une explication intuitive du phénomène, inspirée par Ian Stewart. Supposons que l'on choisisse au hasard une rue, puis ensuite, toujours au hasard, une maison dans cette rue, et que l'on regarde le premier chiffre de son numéro.
Si la rue contient 19 maisons, il y a 10 fois plus de maisons dont le nombre commence par "1" plutôt que par "9". Si la rue contient 47 maisons, il y a toujours beaucoup plus de maisons commençant par "1" plutôt que par "9". Le nombre "9" finit péniblement par rattraper son retard lorsque l'on en arrive à considérer des rues ayant entre 90 et 100 maisons, mais ce retard recommence à se creuser dès que l'on entre dans le domaine des maisons contenant entre 100 et 200 maisons ! Bref, les petits chiffres sont toujours en avance sur les grands, ce qui leur confère une présence plus fréquente que ces derniers.
|
Roger rame sur la rivière
Roger habite près d'une rivière qui en hiver a un assez fort courant alors qu'il est quasi nul en été.
En hiver, Roger met
2 heures pour descendre le courant jusqu'à un certain point
et 3 heures pour remonter contre le courant à son point de départ.
Combien mettra-t-il de temps en été pour faire le même parcours (aller ou retour)?
(On suppose évidemment qu'il rame toujours à la même allure.)
Montrer/cacher la solution de cette énigme
La solution de l'énigme Roger rame sur la rivière :
Deux heures et 24 minutes.
Explication:
distance = vitesse * temps
d = distance parcourue
V = vitesse à laquelle Roger rame
v = vitesse du courant de la rivière en hiver
ta = temps pour le parcours aller en hiver, avec le courant
tr = temps pour le parcours retour en hiver, contre le courant
te = temps pour le parcours en été, en eau calme (identique pour l'aller et le retour)
1 On calcule d'abord les vitesses relatives de Roger ramant en eau calme et du courant de la rivière en hiver.
d = (V+v) * ta = (V-v) * tr
(V+v) * 2 = (V-v) * 3
2V + 2v = 3V - 3v
V = 5v
Roger rame donc cinq fois plus vite que le courant.
2 On calcule ensuite la distance parcourue (identique dans les deux sens, bien sûr).
On supposera que la vitesse du courant de la rivière est égale à x km/h...
d = (V+v) * ta = (5x +1x) * 2 = 12x km
d = (V-v) * tr = (5x - 1x) * 3 = 12x km
Roger rame donc sur une distance de 12x km dans chaque sens.
3 On calcule le temps nécessaire pour parcourir la distance en été.
d = V * te = 5x km/h * te
12x km = 5x km/h * te
te = 12x km / 5x km/h = 12/5 h = 2,4 h = 2 h 24
Roger rame alors pendant 2 h et 24 minutes dans chaque sens, en été.
(On voit que la vitesse x du courant s'annule à la fin, permettant de déterminer
le temps avec précision sans toutefois connaître la véritable distance parcourue...)
|
Les nénuphars
Dans un étang, un nénuphar double à chaque jour.
Il met 100 jours à recouvrir tout l'étang.
Combien de temps mettront deux nénuphars dans les mêmes conditions?
Montrer/cacher la solution de cette énigme
La solution de l'énigme Les nénuphars :
Après une journée, le nénuphar de départ a doublé: il recouvre deux fois plus d'espace.
Si on débute avec deux nénuphars au lieu d'un seul, c'est comme si l'opération était rendue au deuxième jour lorsqu'on débute avec un seul.
Ainsi, débuter avec deux nénuphars revient à écourter d'une journée le travail d'un seul.
Deux nénuphars prendront donc une journée de moins, soit 99 pour recouvrir l'étang.
|
La rosace
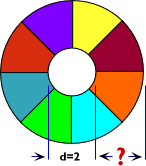
Un architecte planifie une rosace pour une chapelle.
Son esthétique dicte que la surface de chaque panneau externe
doit être égale à la surface du panneau rond central.
Le panneau rond central a un diamètre de deux unités.
On peut ignorer l'épaisseur des montants entre les panneaux.
Quelle doit être la longueur des montants
séparant les panneaux externes?
Montrer/cacher la solution de cette énigme
La solution de l'énigme La rosace :
Puisqu'il y a 8 panneaux externes, chacun devant avoir la même surface que le panneau rond central, la surface totale de la rosace doit être 9 fois la surface du panneau central.
La surface d'un cercle est proportionnelle au carré de son rayon: S = * R2.
Ainsi, si la surface totale est 9 fois la surface du panneau rond central, le rayon total de la rosace est 3 fois celui du panneau central.
Vu que le diamètre du panneau central est d=2 unités, son rayon est r=1 unité.
Donc, les montants doivent mesurer (3-1) = 2 unités.
|
|
|
|
| |
|
|
| |


